On Inductive Biases That Enable Generalization of Diffusion Transformers

Jie An^1,2*, Andy (De) Wang¹, Pengsheng Guo¹, Jiebo Luo², Alexander Schwing¹

¹Apple, ²University of Rochester

^*Work done during an internship at Apple

Jacobian eigenvectors of (a) a simplified one-channel UNet [1], (b) the UNet introduced in improved diffusion [2], and (c) a DiT [3]. Kadkhodaie et al. [1] find that the generalization of a UNet-based diffusion model is driven by geometry-adaptive harmonic bases (a), which display oscillatory patterns whose frequency increases as the eigenvalue $\lambda_i$ decreases. We observe similar harmonic bases in split-channel eigenvectors (b) with standard UNets [2]. However, a DiT [3] does not exhibit such harmonic bases (c), motivating our investigation to find the inductive bias that enables generalization in a DiT. The RGB channels of the split-channel eigenvectors are outlined with red, green, and blue boxes, respectively. All models operate directly in the pixel space without applying the patchify operation.

Abstract

Recent work studying the generalization of diffusion models with UNet-based denoisers reveals inductive biases that can be expressed via geometry-adaptive harmonic bases. However, in practice, more recent denoising networks are often based on transformers, e.g., the diffusion transformer (DiT). This raises the question: do transformer-based denoising networks exhibit inductive biases that can also be expressed via geometry-adaptive harmonic bases? To our surprise, we find that this is not the case. This discrepancy motivates our search for the inductive bias that can lead to good generalization in DiT models. Investigating a DiT’s pivotal attention modules, we find that locality of attention maps are closely associated with generalization. To verify this finding, we modify the generalization of a DiT by restricting its attention windows. We inject local attention windows to a DiT and observe an improvement in generalization. Furthermore, we empirically find that both the placement and the effective attention size of these local attention windows are crucial factors. Experimental results on the CelebA, ImageNet, and LSUN datasets show that strengthening the inductive bias of a DiT can improve both generalization and generation quality when less training data is available.

Analyzing the Inductive Biases of Diffusion Models

We compare the generalization ability of a DiT [2] and a UNet [3], two of the most popular diffusion model backbones. Subsequently, we investigate the inductive biases that drive their generalization.

Comparing DiT and UNet Generalization

We compare the generalization of pixel-space DiT and UNet with the same FLOPs for different training image quantities ($N$) using as a metric the PSNR gap proposed by Kadkhodaie et al. [1]. As shown in above figure, when $N{=}10^5$, both DiT and UNet show small PSNR gaps between the training and testing sets. Nevertheless, when $N{=}10^3$ and $N{=}10^4$, a DiT exhibits smaller PSNR gaps compared to a UNet, indicating a better generalization ability under insufficient training data. All PSNR and PSNR gap curves are averaged over three models trained on different dataset shuffles. The standard deviations, illustrated by the curve shadows in the zoomed-in windows, are negligible, indicating minimal variation.

DiT Does Not Have Geometry-Adaptive Harmonic Bases

Can the potential difference in harmonic bases between a DiT and a UNet account for their generalization differences? To answer this question, we follow the approach of [1] and perform an eigendecomposition of the Jacobian matrices for a three-channel classic UNet and a DiT.

The above figure presents the eigenvalues and eigenvectors of a UNet and a DiT with equivalent FLOPs trained with $10$ and $10^5$ images, respectively. (a) The eigenvectors of a UNet tend to memorize the training images when $N{=}10$ and drive the generalization througth harmonic bases [1] when $N{=}10^5$. In contrast, (b) the DiT’s eigenvectors exhibit neither the memorization effect at $N{=}10$ nor harmonic bases at $N{=}10^5$, which indicates that the geometry-adaptive harmonic bases are NOT the inductive bias that drives DiT's generalization.

How Does a DiT Generalize?

The generalization of a DiT may originate from the self-attention dynamics because of its pivotal role in a DiT. Could the attention maps of a DiT provide insights into its inductive biases? In light of this, we empirically compare the attention maps of DiTs with varying levels of generalization: three DiT models trained with $10$, $10^3$, and $10^5$ images, where a DiT trained with more images demonstrates stronger generalization.

The above figure shows attention maps of DiTs trained with $10$, $10^3$, and $10^5$ images. All attention maps are linearly normalized to the range $\left[0, 1\right]$, with a colormap applied to the interval $\left[0, 0.1\right]$ for enhanced visualization. The top-right insets provide a zoomed-in view of the center patch of each attention map. As the number of training images increases, DiT’s generalization improves, and attention maps across all layers exhibit stronger locality. The pink boxes highlight the attention corresponding to a specific output token, obtained by reshaping a single row from the layer-$12$ attention map (original shape: $1{\times}(HW)$) into a matrix of shape $H{\times}W$. As $N$ increases from $10$ to $10^5$, the token attentions progressively concentrate around the region near the output token (highlighted with blue boxes), which indicates that a DiT's generalization arises when the locality of its attention maps becomes stronger.

Injecting Inductive Bias by Restricting Attention Windows

To verify that the locality of attention maps enables the generalization of a DiT, we hypothesize that it’s possible to adjust the inductive bias of a DiT by restricting attention windows.

Attention Window Restriction

Local attention, initially proposed to enhance computational efficiency, is a straightforward yet effective way to modify a DiT's generalization.

The above figure compares the global and local attention maps: (a) global attention captures the relationship between the target token and any input token, whereas (b) local attention focuses only on tokens within a nearby window around the target.

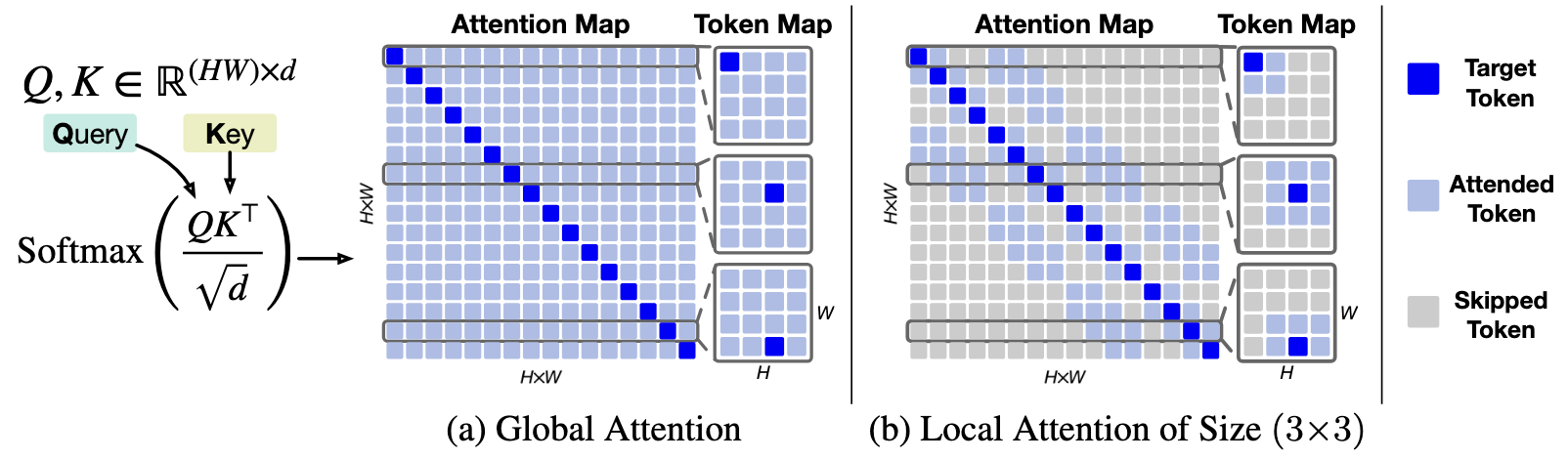
Applying Local Attentions to a DiT

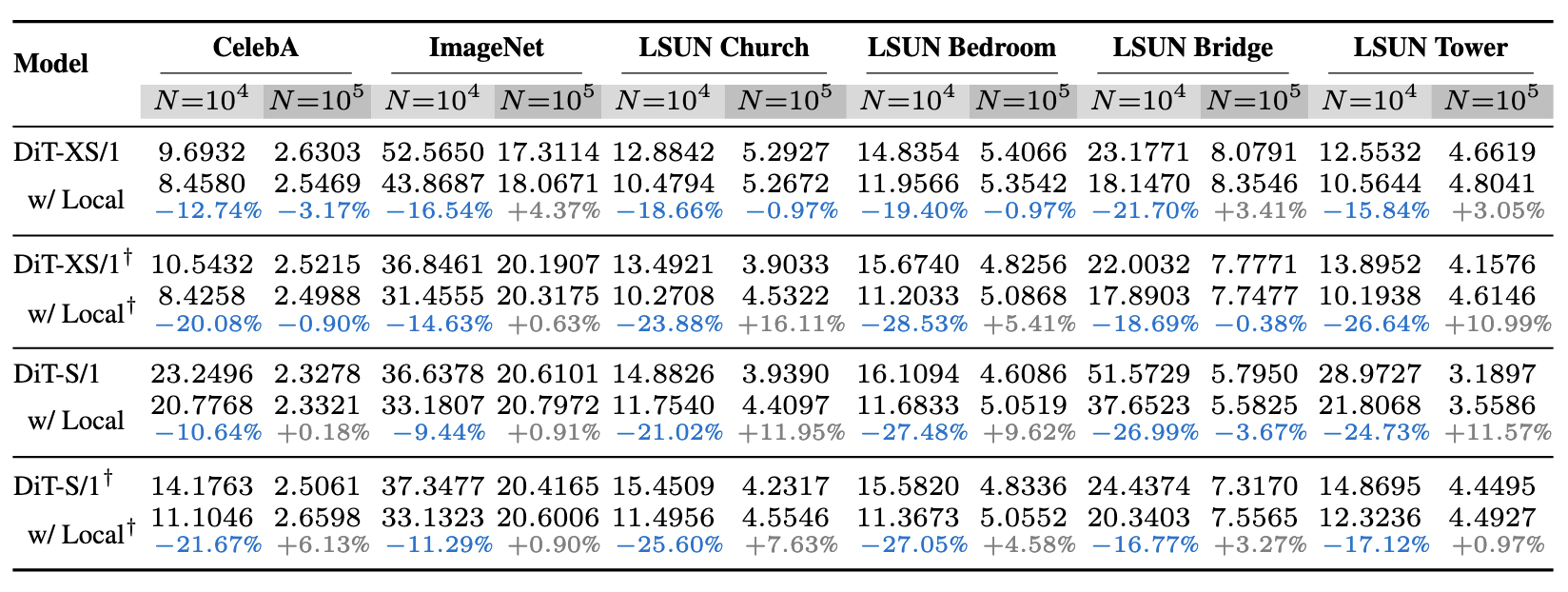
Using local attentions in a DiT can consistently improve its generalization (measured by PSNR gap) across different datasets and model sizes.

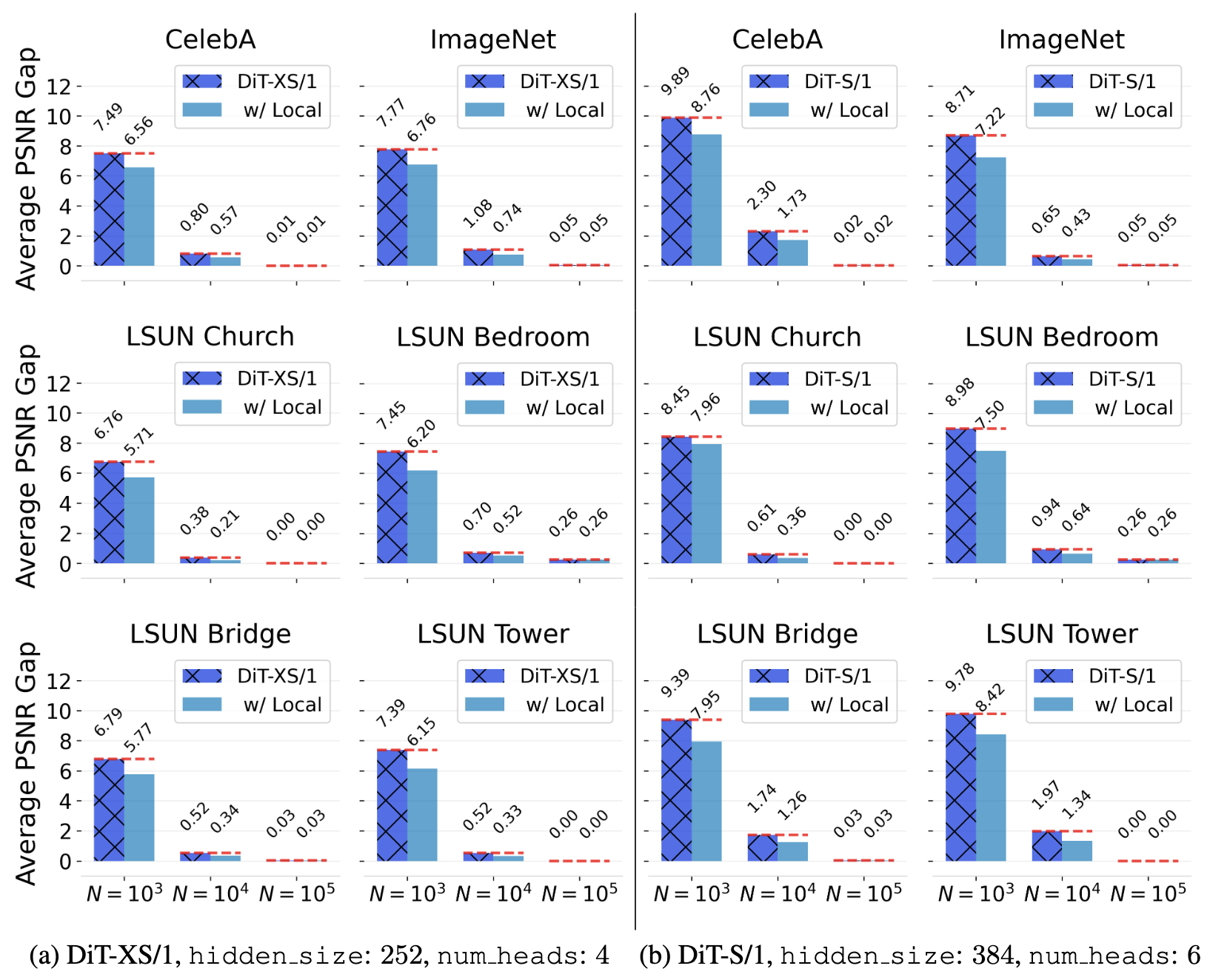
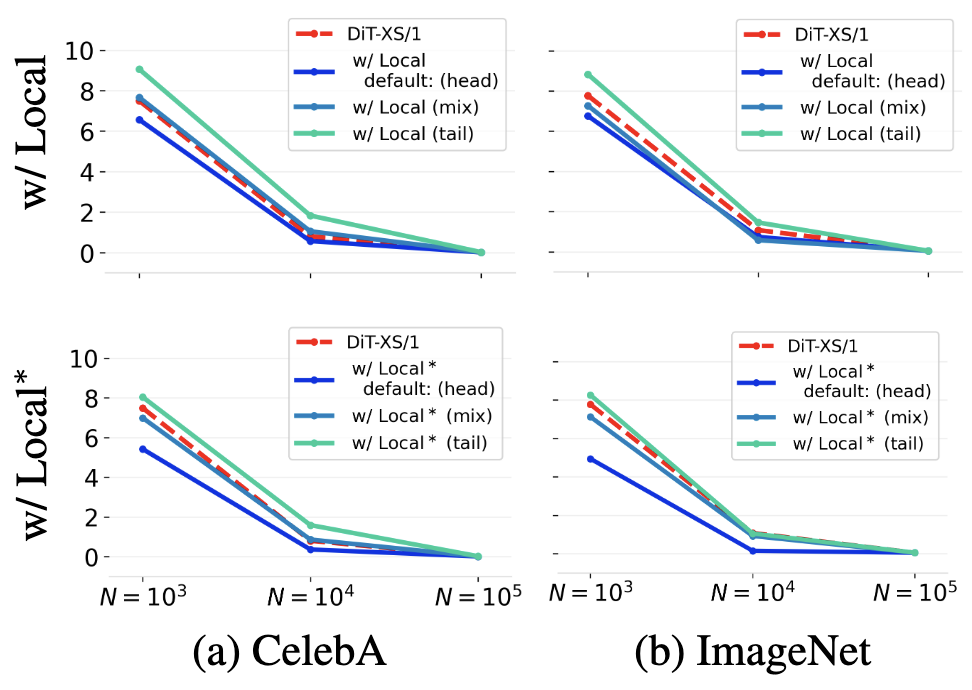
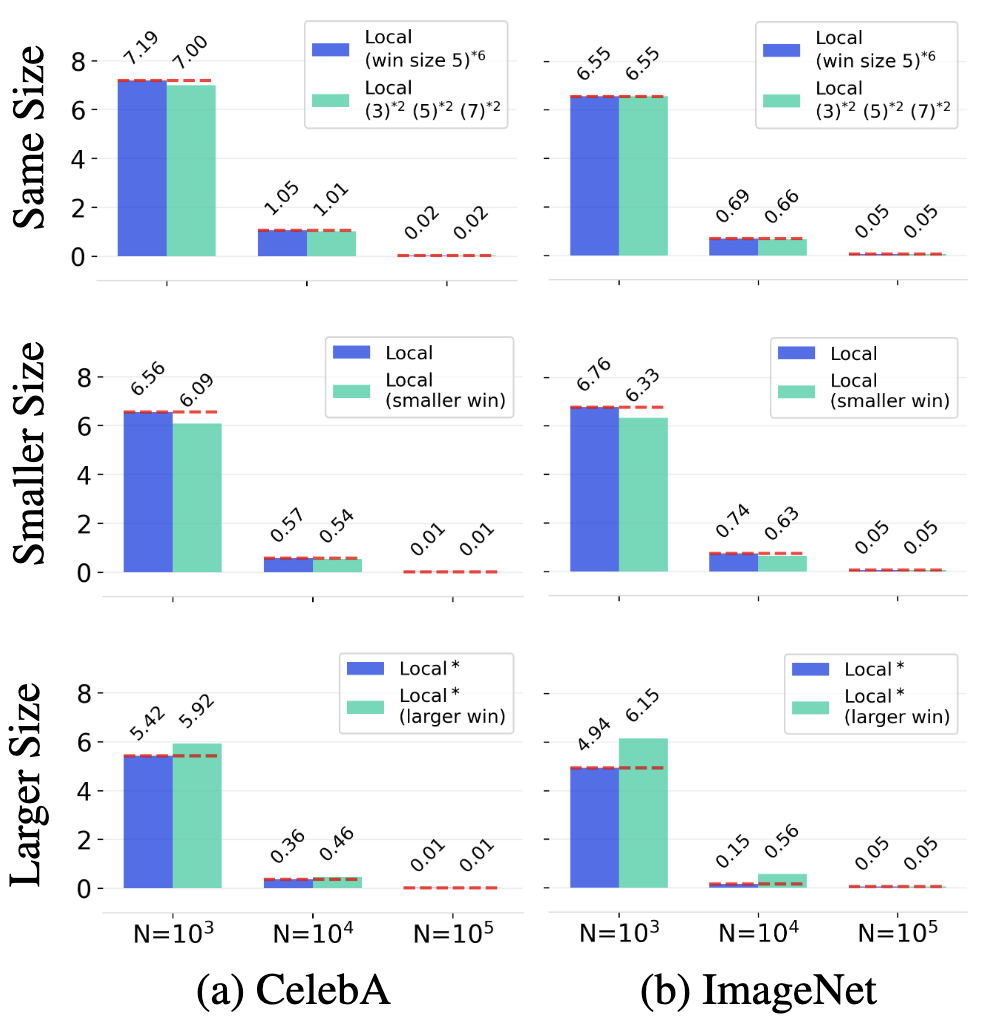
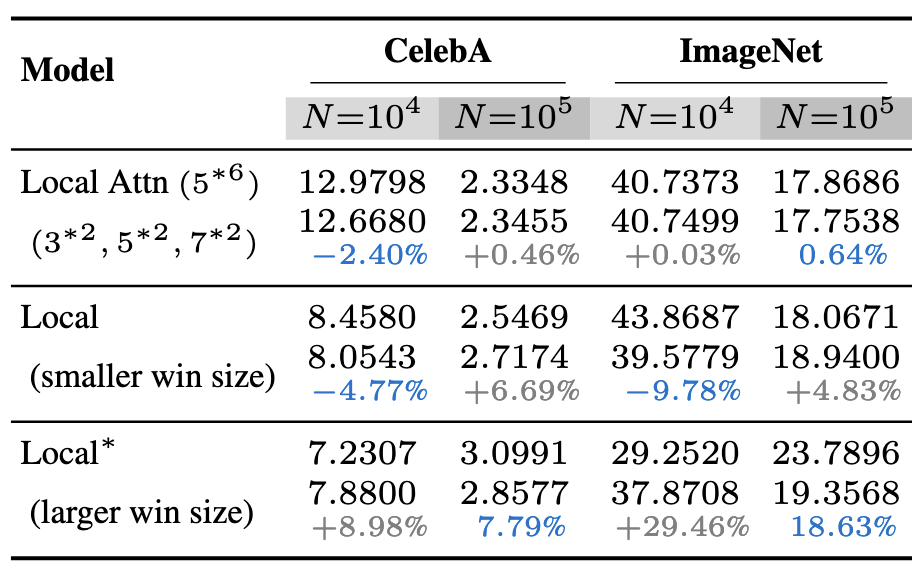
The above figure shows the PSNR gap$\downarrow$ comparison between a standard DiT and a DiT equipped with local attention for two architectures: (a) DiT-XS/1 and (b) DiT-S/1. Incorporating local attention reduces the PSNR gap consistently across $N{=}10^3$, $N{=}10^4$, and $N{=}10^5$. This advantage is robust across six different datasets and both DiT backbones. In this setup, local attention with window sizes $\left(3, 5, 7, 9, 11, 13\right)$ is applied to the first six layers of the DiT. Textured bars highlight the default DiT baselines.

For a discriminative model, e.g., a classifier, better generalization typically leads to better model performance when the training dataset is insufficient. Is this also the case for generative models like a DiT?

The above table shows the FID$\downarrow$ comparison between a standard DiT and a DiT equipped with local attention. $^\dagger$ indicates training with different random seeds, train-test splits, and doubled batch sizes. For the DiT-XS/1 and DiT-S/1 architectures, local attention reduces FID when the DiT’s generalization is not saturated ($N{=}10^4$). At $N{=}10^5$, local attention achieves comparable or marginally higher FID compared to the standard DiT. These findings are consistent across various datasets, random seeds, train-test splits, and batch sizes. In this setting, local attention with window sizes of $\left(3, 5, 7, 9, 11, 13\right)$ is applied to the first six layers of the DiT, where both the placement and window size play a crucial role in determining a DiT's FID result. Further details are provided below.

Placement of Attention Window Restriction

Given the same set of local attentions, placing them at different layers of a DiT leads to different results.

The above figure shows the PSNR gap$\downarrow$ comparison for different local attention placement patterns. We find that placing local attention in the early layers (head) results in a smaller PSNR gap compared to mixing local and global attention (mix) or applying local attention in the later layers (tail). The latter two configurations may even perform worse than the vanilla DiT.

The results measured by PSNR gap are also verified by FID values.

The above table shows the FID$\downarrow$ comparison for different local attention placement patterns. Local$^\ast$ represents using nine local attention layers with window sizes $\left( 3^{*3}, 5^{*3}, 7^{*3} \right)$ in a DiT. Placing local attention in the early layers achieves lower FIDs when $N{=}10^4$, indicating successful generalization modification. In contrast, mix and tail placements fail to consistently modify the generalization of a DiT. The lowest FIDs are highlighted in bold.

Effective Attention Window Size

Adjusting the effective attention window size provides an additional mechanism to control the generalization of a DiT.

The above figure shows the PSNR gap$\downarrow$ changes when the effective attention window size is kept constant, decreased, or increased. Reducing the window size results in a smaller PSNR gap, indicating improved generalization.

We also compare the FID values when changing the effective attention window size.

The above table shows the FID$\downarrow$ changes when the effective attention window size is kept constant, decreased, or increased. Modifying the attention window distribution while keeping the overall window size unchanged results in minimal FID changes when $N{=}10^4$. Decreasing the window size improves generalization, leading to lower FID at $N{=}10^4$, whereas increasing the window size has the opposite effect.

BibTeX

will be changed to our citation

@article{an2024ditgeneralization,
                    title   = {On Inductive Biases That Enable Generalization of Diffusion Transformers}, 
                    author  = {Jie An and De Wang and Pengsheng Guo and Jiebo Luo and Alexander Schwing},
                    journal = {arXiv preprint arXiv:2410.21273},
                    year    = {2024},
                    }

References

[1] Zahra Kadkhodaie, Florentin Guth, Eero P Simoncelli, and Stéphane Mallat. Generalization in diffusion models arises from geometry-adaptive harmonic representation. In ICLR, 2024.

[2] Alexander Quinn Nichol and Prafulla Dhariwal. Improved denoising diffusion probabilistic models. In ICML, 2021.

[3] William Peebles and Saining Xie. Scalable diffusion models with transformers. In CVPR, 2023.